Activity 8: Morphological Operations

Mathematical morphology is a set-theoretical approach to multi-dimensional digital signal or image analysis, based on shape. The signals are locally compared with so-called structuring elements S of arbitrary shape with a reference point R.

The eroded image of an object O with respect to a structuring element S with a reference point R, , is the set of all reference points for which S is completely contained in O.

The dilated image of an object O with respect to a structuring element S with a reference point R, , is the set of all reference points for which O and S have at least one common point.

Here are some examples of images that are eroded and dilated:

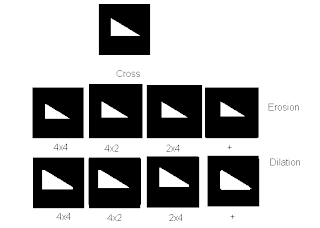
I would like to acknowledge Rafael Jaculbia for lending me his image templates I used in getting the erosion and dilation. I also acknowledge Billy Narag and Abraham Latimer Camba for helping understand idea of dilation and erosion.

For this activity, I would give myself a grade of 9 for the reason that I am not sure of some of my results because I did not correspond on my guess image.

Reference:
http://ikpe1101.ikp.kfa-juelich.de/briefbook_data_analysis/node178.html